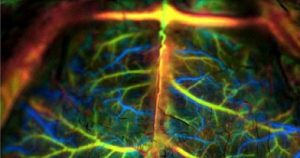
Pensar fora da caixa em uma área que poderia em si ser colocada “fora da caixa” como a física quântica parece um pouco complicado. Mas, mesmo neste campo do conhecimento, é preciso inovar – principalmente em se tratando de problemas para os quais as soluções propostas ainda estão longe de serem satisfatórias. Foi isso que fez Diego Paiva Pires em seu trabalho de doutorado no Instituto de Física de São Carlos (IFSC) da USP, premiado como Tese Destaque este ano na categoria “Exatas”.
O problema que ele atacou foi determinação de um limite mínimo no tempo de evolução entre estados de um dado sistema quântico, o que se relaciona à máxima velocidade dessa mudança, conhecida como quantum speed limit (QSL). E a ferramenta proposta para abordá-lo foi a geometria da informação – algo até então não explorado em profundidade na literatura.
A importância prática dos resultados obtidos devem aparecer lá na frente. Determinar o quão rápido um sistema quântico evolui pode ajudar em melhores escolhas dos cientistas que trabalham no desenvolvimento da computação quântica, com o objetivo de processar informações ainda mais rápido. Que é o que os computadores quânticos prometem: capacidade e velocidade de processamento sem precedentes.
Mudanças velozes
Mas o que é um estado quântico e como ele é alterado? Primeiro, tenha em mente que a física quântica lida com partículas do mundo subatômico, não regidas pelas mesmas leis da mecânica clássica. Entre elas prótons, elétrons e fótons.
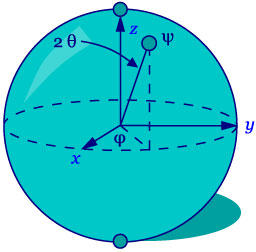
Dito isso, sabemos que essas partículas apresentam determinadas propriedades físicas que podem sofrer perturbações e serem modificadas. Um exemplo de propriedade é o spin, o sentido de rotação de um elétron. Já a perturbação seria, num acelerador, fazer a partícula passar por um campo magnético.
Ao se verificar o estado do sistema antes e após a perturbação, pode-se concluir que o spin foi alterado. “Existem maneiras de, matematicamente, medirmos essas alterações, que chamamos de alterações dos estados quânticos”, explica Diogo de Oliveira Soares Pinto, professor do IFSC e orientador de Diego Pires no doutorado. “Os estados de spin, inclusive, são o que usamos para codificar os bits quânticos, q-bits”, ressalta, lembrando que na computação quântica, ao invés de zero ou um, como os bits clássicos, temos os q-bits, que podem ser zero, um, ou qualquer combinação ou superposição de zeros e uns.
Voltando ao nosso sistema, poderíamos supor que, em sistemas equivalentes, sofrendo iguais perturbações, o tempo para ocorrer uma determinada alteração de um estado para outro (neste caso, a mudança de spin) seria o mesmo. Mas não é assim que acontece. Na mecânica quântica, que trabalha com probabilidades, não existe uma forma precisa de calcular isso. “O mais longe que podemos ir é estimar um tempo mínimo para que isso aconteça”, diz Diego Pires. Mas mesmo isso não é tão simples. Assim, sua pesquisa procurou uma forma mais adequada para calcular esse tempo mínimo, ou, se preferir, a máxima velocidade em que a modificação do estado quântico pode ocorrer. “Diante de problemas como os da mecânica quântica, temos que comparar os ‘diferentes jeitos de fazer a conta’ e escolher o que melhor se aplica a cada um, e foi o que o Diego fez nesse trabalho”, resume o professor Diogo Pinto, justificando a escolha da geometria como ferramenta para os cálculos.
E ajudar a determinar a máxima velocidade da passagem entre estados quânticos, poderá, em um futuro não tão distante, ser útil aos físicos experimentais, cientistas da computação, e engenheiros da computação que elaboram sistemas para aplicação em computação quântica. Alterando algumas configurações do sistema, seria possível atingir uma maior velocidade de mudança de estado, com o objetivo de acelerar também o processamento das informações. Mas o trabalho pode trazer contribuições também para outros campos da física quântica, como a termodinâmica e a metrologia quântica e estudo de emaranhamento.
O lugar da geometria
Várias tentativas de solucionar a questão do limite quântico de velocidade têm sido feitas, mas seus resultados deixaram lacunas ou mesmo inconsistências quando comparados entre si. O pulo do gato da pesquisa do físico do IFSC foi utilizar a geometria para tratar do problema. Mais especificamente, da geometria da informação, uma área da matemática que utiliza ferramentas geométricas no estudo de modelos estatísticos. Vale lembrar que, no “mundo estranho” da física quântica, onde as leis clássicas não se aplicam, trabalha-se bastante com probabilidade. Mas, mesmo assim, é possível atingir resultados bem consistentes. “A mecânica quântica, por mais contra-intuitiva que possa parecer, oferece resultados consistentes e coerentes com os experimentos feitos até hoje na escala de energias em que a teoria é estabelecida”, ressalta Diego Pires.00
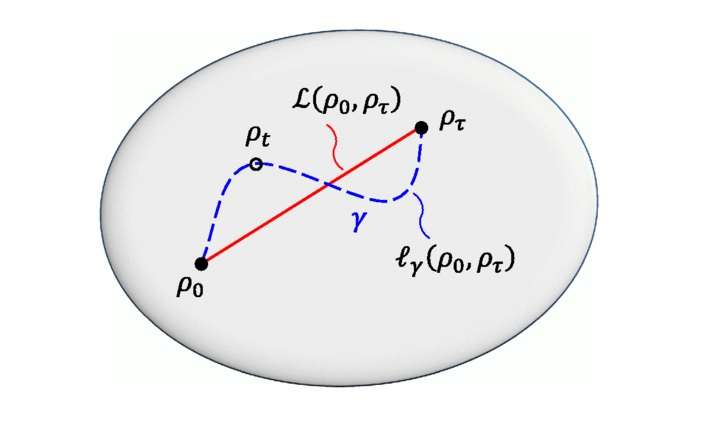
Para se determinar o quão rápido um sistema pode evoluir de um estado para outro, é necessário poder distinguir este estado do outro. E como, matematicamente, isso pode ser feito? “Do ponto de vista geométrico, as ‘medidas de distinguibilidade’ (formas de aferir o quão distante um estado está do outro) funcionam como réguas. É como se cada estado quântico fosse um pontinho num papel, daí eu pego uma régua e meço a distância entre eles”, detalha o professor Diogo Pinto.
Como estamos falando de mecânica quântica, a solução não é trivial. Mesmo assim, a linguagem da geometria foi o arsenal que se mostrou mais interessante para enfrentar o problema. Ainda utilizando a mesma analogia, o docente explica que existe uma família infinita de réguas, isto é, infinitas maneiras de calcular a distância entre esses pontos. O trabalho mostrou como isso repercute no limite quântico de velocidade e, consequentemente, no limite mínimo de tempo.
Até então existiam soluções pontuais para este problema, bem específicas para situações bem específicas. Um dos maiores diferenciais da tese, na opinião do professor, foi mostrar como, com o uso da boa e velha geometria é possível atacar o problema de uma forma mais geral, que pode ser aplicada em diferentes contextos, como sistemas físicos mais complexos. Diego Paiva concorda: “através de um teorema simples, mas robusto, conseguimos formular em termos geométricos toda esta discussão sobre o tempo, além de recobrar e generalizar resultados já reportados na literatura.”
Além da tese premiada, os estudos culminaram na publicação de artigos científicos com colaboração internacional em periódicos relevantes da área, como Physical Review X e Physical Review A.
O pesquisador comentou em mais detalhes sua pesquisa em um vídeo postado nesta página da Pró-Reitoria de Pós-Graduação.
Mais informações: e-mail diegopaivapires@gmail.com